How to Draw Moore State Diagram

Finite-state machine whose output values are determined only by its current land

In the theory of computation, a Moore machine is a finite-country machine whose current output values are adamant only by its current land. This is in contrast to a Mealy car, whose output values are determined both by its current state and by the values of its inputs. Similar other finite state machines, in Moore machines, the input typically influences the next state. Thus the input may indirectly influence subsequent outputs, simply non the current or firsthand output. The Moore machine is named after Edward F. Moore, who presented the concept in a 1956 paper, "Gedanken-experiments on Sequential Machines."^[1]

Formal definition [edit]

A Moore machine can be divers every bit a vi-tuple ${\displaystyle (Q,q_{0},\Sigma ,O,\delta ,One thousand)}$ consisting of the following:

A Moore machine can be regarded as a restricted type of finite-country transducer.

Visual representation [edit]

Tabular array [edit]

State transition tabular array is a tabular array showing relation between an input and a country.^{[ clarification needed ]}

Diagram [edit]

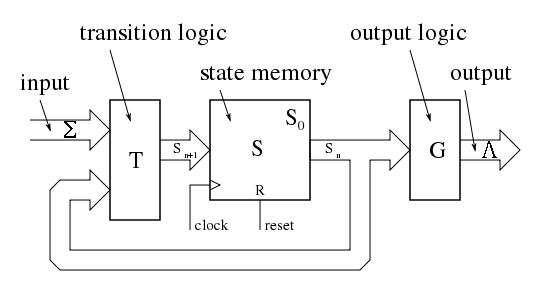
The country diagram for a Moore machine or Moore diagram is a diagram that associates an output value with each land. Moore automobile is an output producer.

Relationship with Mealy machines [edit]

As Moore and Mealy machines are both types of finite-state machines, they are equally expressive: either type tin can be used to parse a regular language.

The deviation between Moore machines and Mealy machines is that in the latter, the output of a transition is determined by the combination of current state and current input ( ${\displaystyle South\times \Sigma }$ as the input to ${\displaystyle G}$ ), as opposed to simply the electric current state ( ${\displaystyle South}$ equally the input to ${\displaystyle Yard}$ ). When represented as a state diagram,

• for a Moore motorcar, each node (land) is labeled with an output value;
• for a Mealy car, each arc (transition) is labeled with an output value.

Every Moore machine ${\displaystyle Thou}$ is equivalent to the Mealy machine with the aforementioned states and transitions and the output function ${\displaystyle G(due south,\sigma )\rightarrow G_{K}(\delta _{M}(s,\sigma ))}$ , which takes each country-input pair ${\displaystyle (southward,\sigma )}$ and yields ${\displaystyle G_{M}(\delta _{M}(s,\sigma ))}$ , where ${\displaystyle G_{M}}$ is ${\displaystyle Thousand}$ 'southward output function and ${\displaystyle \delta _{M}}$ is ${\displaystyle M}$ 's transition function.

However, non every Mealy machine tin can be converted to an equivalent Moore machine. Some can be converted only to an almost equivalent Moore auto, with outputs shifted in time. This is due to the way that land labels are paired with transition labels to form the input/output pairs. Consider a transition ${\displaystyle s_{i}\rightarrow s_{j}}$ from state ${\displaystyle s_{i}}$ to state ${\displaystyle s_{j}}$ . The input causing the transition ${\displaystyle s_{i}\rightarrow s_{j}}$ labels the edge ${\displaystyle (s_{i},s_{j})}$ . The output corresponding to that input, is the label of land ${\displaystyle s_{i}}$ .^[ii] Detect that this is the source state of the transition. So for each input, the output is already fixed before the input is received, and depends solely on the nowadays state. This is the original definition by East. Moore. It is a common mistake to use the label of state ${\displaystyle s_{j}}$ equally output for the transition ${\displaystyle s_{i}\rightarrow s_{j}}$ .

Examples [edit]

Types according to number of inputs/outputs.

Simple [edit]

Simple Moore machines have one input and one output:

• border detector using XOR
• binary calculation machine
• clocked sequential systems (a restricted form of Moore car where the country changes only when the global clock betoken changes)

Nigh digital electronic systems are designed every bit clocked sequential systems. Clocked sequential systems are a restricted form of Moore machine where the land changes only when the global clock signal changes. Typically the current state is stored in flip-flops, and a global clock signal is connected to the "clock" input of the flip-flops. Clocked sequential systems are ane fashion to solve metastability problems. A typical electronic Moore machine includes a combinational logic chain to decode the current country into the outputs (lambda). The instant the electric current state changes, those changes ripple through that chain, and almost instantaneously the output gets updated. There are blueprint techniques to ensure that no glitches occur on the outputs during that brief menstruum while those changes are rippling through the chain, but most systems are designed and so that glitches during that brief transition time are ignored or are irrelevant. The outputs and so stay the same indefinitely (LEDs stay vivid, power stays connected to the motors, solenoids stay energized, etc.), until the Moore machine changes country once again.

Worked Example [edit]

A sequential network has one input and one output. The output becomes 1 and remains 1 thereafter when at least 2 0's and two i'due south take occurred every bit inputs.

A Moore machine with 9 states for the above description is shown on the right. The initial state is state A, and the final state is state I. The state table for this instance is every bit follows:

Electric current state	Input	Next state	Output
A	0	D	0
	1	B
B	0	E	0
	one	C
C	0	F	0
	1	C
D	0	G	0
	i	Due east
E	0	H	0
	i	F
F	0	I	0
	1	F
Thousand	0	One thousand	0
	ane	H
H	0	H	0
	one	I
I	0	I	1
	ane	I

Circuitous [edit]

More circuitous Moore machines can have multiple inputs likewise as multiple outputs.

Gedanken-experiments [edit]

In Moore's paper "Gedanken-experiments on Sequential Machines",^[1] the ${\displaystyle (n;1000;p)}$ automata (or machines) ${\displaystyle S}$ are defined as having ${\displaystyle north}$ states, ${\displaystyle m}$ input symbols and ${\displaystyle p}$ output symbols. Nine theorems are proved near the structure of ${\displaystyle S}$ , and experiments with ${\displaystyle South}$ . Later, " ${\displaystyle S}$ machines" became known as "Moore machines".

At the end of the paper, in Section "Further bug", the following job is stated:

Some other directly following trouble is the improvement of the bounds given at the theorems 8 and 9.

Moore's Theorem 8 is formulated every bit:

Given an arbitrary ${\displaystyle (n;m;p)}$ machine ${\displaystyle S}$ , such that every ii of its states are distinguishable from one another, then there exists an experiment of length ${\displaystyle {\tfrac {n(n-ane)}{2}}}$ which determines the land of ${\displaystyle S}$ at the cease of the experiment.

In 1957, A. A. Karatsuba proved the following ii theorems, which completely solved Moore's problem on the improvement of the bounds of the experiment length of his "Theorem 8".

Theorem A. If ${\displaystyle S}$ is an ${\displaystyle (n;chiliad;p)}$ machine, such that every two of its states are distinguishable from one some other, then there exists a branched experiment of length at nearly ${\displaystyle {\tfrac {(due north-1)(n-two)}{2}}+1}$ through which ane may decide the state of ${\displaystyle S}$ at the cease of the experiment.

Theorem B. There exists an ${\displaystyle (n;m;p)}$ machine, every two states of which are distinguishable from ane another, such that the length of the shortest experiments establishing the state of the machine at the end of the experiment is equal to ${\displaystyle {\tfrac {(n-1)(n-2)}{2}}+1}$ .

Theorems A and B were used for the basis of the course work of a pupil of the fourth yr, A. A. Karatsuba, "On a problem from the automata theory", which was distinguished past testimonial reference at the contest of student works of the kinesthesia of mechanics and mathematics of Moscow Lomonosow State University in 1958. The paper by Karatsuba was given to the periodical Uspekhi Mat. Nauk on 17 Dec 1958 and was published there in June 1960.^[3]

Until the nowadays 24-hour interval (2011), Karatsuba's outcome on the length of experiments is the only exact nonlinear result, both in automata theory, and in like problems of computational complexity theory.

Come across also [edit]

• Synchronous circuit
• Mealy auto
• Algorithmic state machine
• Autonomous system (mathematics)

References [edit]

1. ^ ^{a b} Moore, Edward F (1956). "Gedanken-experiments on Sequential Machines". Automata Studies, Annals of Mathematical Studies. Princeton, N.J.: Princeton Academy Press (34): 129–153.
2. ^ Lee, Edward Ashford; Seshia, Sanjit Arunkumar (2013). Introduction to Embedded Systems (1.08 ed.). UC Berkeley: Lulu.com. ISBN9780557708574 . Retrieved one July 2014.
3. ^ Karatsuba, A. A. (1960). "Solution of one trouble from the theory of finite automata". Uspekhi Mat. Nauk (fifteen:3): 157–159.

Further reading [edit]

• Conway, J.H. (1971). Regular algebra and finite machines. London: Chapman and Hall. ISBN0-412-10620-5. Zbl 0231.94041.
• Moore Due east. F. Gedanken-experiments on Sequential Machines. Automata Studies, Annals of Mathematical Studies, 34, 129–153. Princeton Academy Press, Princeton, Northward.J.(1956).
• Karatsuba A. A. Solution of i trouble from the theory of finite automata. Usp. Mat. Nauk, fifteen:three, 157–159 (1960).
• Karatsuba A. A. Experimente mit Automaten (German) Elektron. Informationsverarb. Kybernetik, eleven, 611–612 (1975).
• Karatsuba A. A. List of research works.

Moore-and-Mealy-Motorcar

External links [edit]

• Media related to Moore automobile at Wikimedia Commons

fosterwomess.blogspot.com

Source: https://en.wikipedia.org/wiki/Moore_machine

Share this post